Package g0701_0800.s0785_is_graph_bipartite

Class Solution

  • public class Solution
extends Object
    785 - Is Graph Bipartite?

    .

    Medium

    There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:

    • There are no self-edges (graph[u] does not contain u).
    • There are no parallel edges (graph[u] does not contain duplicate values).
    • If v is in graph[u], then u is in graph[v] (the graph is undirected).
    • The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them.

    A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.

    Return true if and only if it is bipartite.

    Example 1:

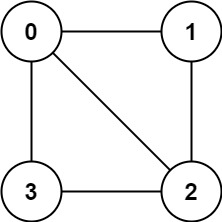
    Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]

    Output: false

    Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.

    Example 2:

    Input: graph = [[1,3],[0,2],[1,3],[0,2]]

    Output: true

    Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.

    Constraints:

    • graph.length == n
    • 1 <= n <= 100
    • 0 <= graph[u].length < n
    • 0 <= graph[u][i] <= n - 1
    • graph[u] does not contain u.
    • All the values of graph[u] are unique.
    • If graph[u] contains v, then graph[v] contains u.

    • Constructor Detail

      • Solution

        public Solution()

    • Method Detail

      • isBipartite

        public boolean isBipartite​(int[][] graph)