Package g1601_1700.s1627_graph_connectivity_with_threshold

Class Solution

java.lang.Object

g1601_1700.s1627_graph_connectivity_with_threshold.Solution

public class Solution
extends Object

1627 - Graph Connectivity With Threshold.

Hard

We have n cities labeled from 1 to n. Two different cities with labels x and y are directly connected by a bidirectional road if and only if x and y share a common divisor strictly greater than some threshold. More formally, cities with labels x and y have a road between them if there exists an integer z such that all of the following are true:

• x % z == 0,
• y % z == 0, and
• z > threshold.

Given the two integers, n and threshold, and an array of queries, you must determine for each queries[i] = [ai, bi] if cities ai and bi are connected directly or indirectly. (i.e. there is some path between them).

Return an array answer, where answer.length == queries.length and answer[i] is true if for the ith query, there is a path between ai and bi, or answer[i] is false if there is no path.

Example 1:

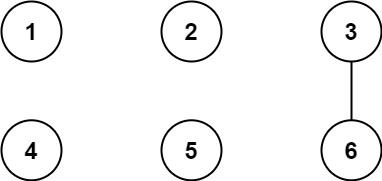
Input: n = 6, threshold = 2, queries = [[1,4],[2,5],[3,6]]

Output: [false,false,true]

Explanation: The divisors for each number:

1: 1

2: 1, 2

3: 1, 3

4: 1, 2, 4

5: 1, 5

6: 1, 2, 3, 6

Using the underlined divisors above the threshold, only cities 3 and 6 share a common divisor, so they are the only ones directly connected. The result of each query:

[1,4] 1 is not connected to 4

[2,5] 2 is not connected to 5

[3,6] 3 is connected to 6 through path 3–6

Example 2:

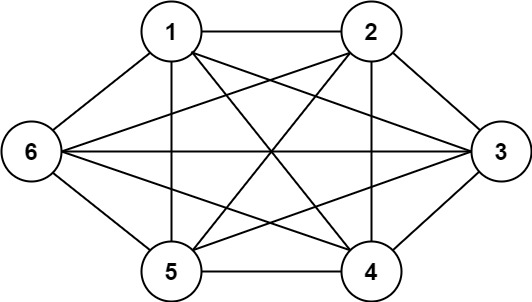
Input: n = 6, threshold = 0, queries = [[4,5],[3,4],[3,2],[2,6],[1,3]]

Output: [true,true,true,true,true]

Explanation: The divisors for each number are the same as the previous example. However, since the threshold is 0, all divisors can be used. Since all numbers share 1 as a divisor, all cities are connected.

Example 3:

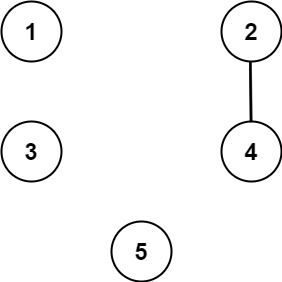
Input: n = 5, threshold = 1, queries = [[4,5],[4,5],[3,2],[2,3],[3,4]]

Output: [false,false,false,false,false]

Explanation: Only cities 2 and 4 share a common divisor 2 which is strictly greater than the threshold 1, so they are the only ones directly connected. Please notice that there can be multiple queries for the same pair of nodes [x, y], and that the query [x, y] is equivalent to the query [y, x].

Constraints:

• 2 <= n <= 104
• 0 <= threshold <= n
• 1 <= queries.length <= 105
• queries[i].length == 2
• 1 <= ai, bi <= cities
• ai != bi

Constructor Summary

Constructors

Constructor	Description
Solution()

Method Summary

Modifier and Type	Method	Description
List<Boolean>	areConnected(int n, int threshold, int[][] queries)

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Detail

Solution

public Solution()

Method Detail

areConnected

public List<Boolean> areConnected(int n,
                                  int threshold,
                                  int[][] queries)