Package g1701_1800.s1766_tree_of_coprimes

Class Solution

  • public class Solution
extends Object
    1766 - Tree of Coprimes.

    Hard

    There is a tree (i.e., a connected, undirected graph that has no cycles) consisting of n nodes numbered from 0 to n - 1 and exactly n - 1 edges. Each node has a value associated with it, and the root of the tree is node 0.

    To represent this tree, you are given an integer array nums and a 2D array edges. Each nums[i] represents the ith node’s value, and each edges[j] = [uj, vj] represents an edge between nodes uj and vj in the tree.

    Two values x and y are coprime if gcd(x, y) == 1 where gcd(x, y) is the greatest common divisor of x and y.

    An ancestor of a node i is any other node on the shortest path from node i to the root. A node is not considered an ancestor of itself.

    Return an array ans of size n, where ans[i] is the closest ancestor to node i such that nums[i] and nums[ans[i]] are coprime , or -1 if there is no such ancestor.

    Example 1:

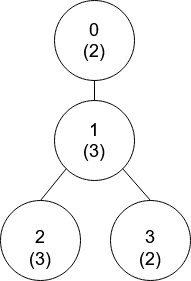
    Input: nums = [2,3,3,2], edges = [[0,1],[1,2],[1,3]]

    Output: [-1,0,0,1]

    Explanation: In the above figure, each node’s value is in parentheses.

    • Node 0 has no coprime ancestors.

    • Node 1 has only one ancestor, node 0. Their values are coprime (gcd(2,3) == 1). - Node 2 has two ancestors, nodes 1 and 0. Node 1’s value is not coprime (gcd(3,3) == 3), but node 0’s value is (gcd(2,3) == 1), so node 0 is the closest valid ancestor.

    • Node 3 has two ancestors, nodes 1 and 0. It is coprime with node 1 (gcd(3,2) == 1), so node 1 is its closest valid ancestor.

    Example 2:

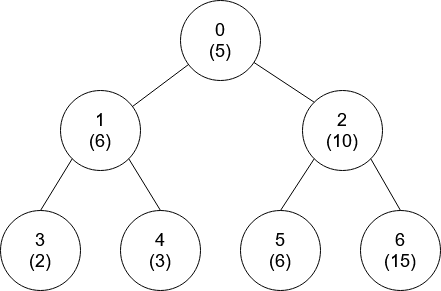
    Input: nums = [5,6,10,2,3,6,15], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]

    Output: [-1,0,-1,0,0,0,-1]

    Constraints:

    • nums.length == n
    • 1 <= nums[i] <= 50
    • 1 <= n <= 105
    • edges.length == n - 1
    • edges[j].length == 2
    • 0 <= uj, vj < n
    • uj != vj

    • Constructor Detail

      • Solution

        public Solution()

    • Method Detail

      • getCoprimes

        public int[] getCoprimes​(int[] nums,
                         int[][] edges)