Package g2601_2700.s2617_minimum_number_of_visited_cells_in_a_grid

Class Solution

  • public class Solution
extends Object
    2617 - Minimum Number of Visited Cells in a Grid.

    Hard

    You are given a 0-indexed m x n integer matrix grid. Your initial position is at the top-left cell (0, 0).

    Starting from the cell (i, j), you can move to one of the following cells:

    • Cells (i, k) with j < k <= grid[i][j] + j (rightward movement), or
    • Cells (k, j) with i < k <= grid[i][j] + i (downward movement).

    Return the minimum number of cells you need to visit to reach the bottom-right cell (m - 1, n - 1). If there is no valid path, return -1.

    Example 1:

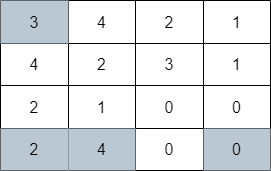
    Input: grid = [[3,4,2,1],[4,2,3,1],[2,1,0,0],[2,4,0,0]]

    Output: 4

    Explanation: The image above shows one of the paths that visits exactly 4 cells.

    Example 2:

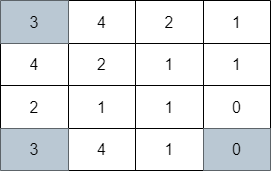
    Input: grid = [[3,4,2,1],[4,2,1,1],[2,1,1,0],[3,4,1,0]]

    Output: 3

    Explanation: The image above shows one of the paths that visits exactly 3 cells.

    Example 3:

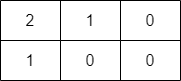
    Input: grid = [[2,1,0],[1,0,0]]

    Output: -1

    Explanation: It can be proven that no path exists.

    Constraints:

    • m == grid.length
    • n == grid[i].length
    • 1 <= m, n <= 105
    • 1 <= m * n <= 105
    • 0 <= grid[i][j] < m * n
    • grid[m - 1][n - 1] == 0

    • Constructor Detail

      • Solution

        public Solution()

    • Method Detail

      • minimumVisitedCells

        public int minimumVisitedCells​(int[][] grid)