Package g0901_1000.s0935_knight_dialer

Class Solution

java.lang.Object
g0901_1000.s0935_knight_dialer.Solution
public class Solution extends Object
935 - Knight Dialer.

Medium

The chess knight has a unique movement , it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an L ). The possible movements of chess knight are shown in this diagaram:

A chess knight can move as indicated in the chess diagram below:

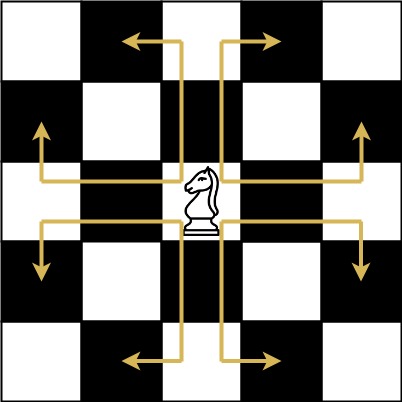
We have a chess knight and a phone pad as shown below, the knight can only stand on a numeric cell (i.e. blue cell).

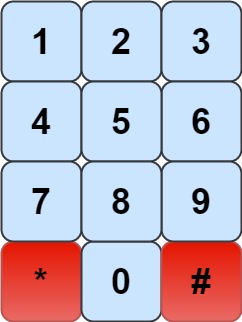
Given an integer n, return how many distinct phone numbers of length n we can dial.

You are allowed to place the knight on any numeric cell initially and then you should perform n - 1 jumps to dial a number of length n. All jumps should be valid knight jumps.

As the answer may be very large, return the answer modulo 109 + 7.

Example 1:

Input: n = 1

Output: 10

Explanation: We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient.

Example 2:

Input: n = 2

Output: 20

Explanation: All the valid number we can dial are [04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]

Example 3:

Input: n = 3131

Output: 136006598

Explanation: Please take care of the mod.

Constraints:

  • 1 <= n <= 5000

  • Constructor Details

    • Solution

      public Solution()

  • Method Details

    • knightDialer

      public int knightDialer(int n)