g1501_1600.s1504_count_submatrices_with_all_ones.Solution

public class Solution extends Object

1504 - Count Submatrices With All Ones.

Medium

Given an m x n binary matrix mat, return the number of submatrices that have all ones.

Example 1:

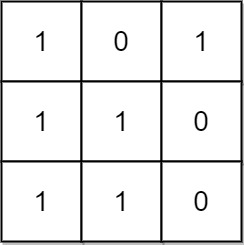
Input: mat = [[1,0,1],[1,1,0],[1,1,0]]

Output: 13

Explanation:

There are 6 rectangles of side 1x1.

There are 2 rectangles of side 1x2.

There are 3 rectangles of side 2x1.

There is 1 rectangle of side 2x2.

There is 1 rectangle of side 3x1.

Total number of rectangles = 6 + 2 + 3 + 1 + 1 = 13.

Example 2:

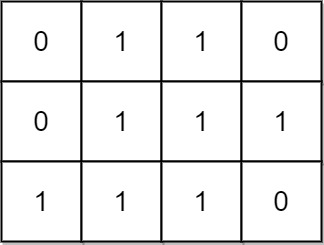
Input: mat = [[0,1,1,0],[0,1,1,1],[1,1,1,0]]

Output: 24

Explanation:

There are 8 rectangles of side 1x1.

There are 5 rectangles of side 1x2.

There are 2 rectangles of side 1x3.

There are 4 rectangles of side 2x1.

There are 2 rectangles of side 2x2.

There are 2 rectangles of side 3x1.

There is 1 rectangle of side 3x2.

Total number of rectangles = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24.

Constraints:

Class Solution

Constructor Summary