g1601_1700.s1632_rank_transform_of_a_matrix.Solution

public class Solution extends Object

1632 - Rank Transform of a Matrix.

Hard

Given an m x n matrix, return a new matrix answer where answer[row][col] is the rank of matrix[row][col].

The rank is an integer that represents how large an element is compared to other elements. It is calculated using the following rules:

The rank is an integer starting from 1.
If two elements p and q are in the same row or column , then:
- If p < q then rank(p) < rank(q)
- If p == q then rank(p) == rank(q)
- If p > q then rank(p) > rank(q)
The rank should be as small as possible.

The test cases are generated so that answer is unique under the given rules.

Example 1:

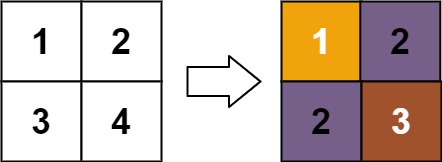
Input: matrix = [[1,2],[3,4]]

Output: [[1,2],[2,3]]

Explanation:

The rank of matrix[0][0] is 1 because it is the smallest integer in its row and column.

The rank of matrix[0][1] is 2 because matrix[0][1] > matrix[0][0] and matrix[0][0] is rank 1.

The rank of matrix[1][0] is 2 because matrix[1][0] > matrix[0][0] and matrix[0][0] is rank 1.

The rank of matrix[1][1] is 3 because matrix[1][1] > matrix[0][1], matrix[1][1] > matrix[1][0], and both matrix[0][1] and matrix[1][0] are rank 2.

Example 2:

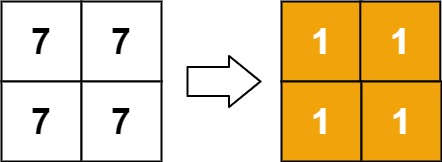
Input: matrix = [[7,7],[7,7]]

Output: [[1,1],[1,1]]

Example 3:

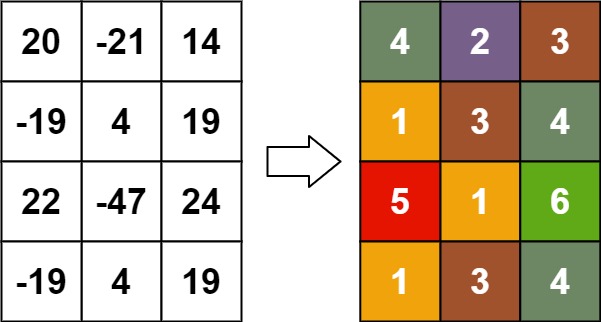
Input: matrix = [[20,-21,14],[-19,4,19],[22,-47,24],[-19,4,19]]

Output: [[4,2,3],[1,3,4],[5,1,6],[1,3,4]]

Constraints:

Constructor Details
- Solution
  
  public Solution()
Method Details
- matrixRankTransform
  
  public int[][] matrixRankTransform(int[][] matrix)

Class Solution

Constructor Summary