Package g3601_3700.s3620_network_recovery_pathways

Class Solution

java.lang.Object

g3601_3700.s3620_network_recovery_pathways.Solution

public class Solution
extends Object

3620 - Network Recovery Pathways.

Hard

You are given a directed acyclic graph of n\u202fnodes numbered from 0\u202fto\u202fn\u202f\u2212\u202f1. This is represented by a 2D array edges of length m, where edges[i] = [ui, vi, costi] indicates a one\u2011way communication from node\u202fui to node\u202fvi with a recovery cost of\u202fcosti.

Some nodes may be offline. You are given a boolean array online where online[i] = true means node\u202fi is online. Nodes 0 and n\u202f\u2212\u202f1 are always online.

A path from 0\u202fto n\u202f\u2212\u202f1 is valid if:

• All intermediate nodes on the path are online.
• The total recovery cost of all edges on the path does not exceed k.

For each valid path, define its score as the minimum edge\u2011cost along that path.

Return the maximum path score (i.e., the largest minimum-edge cost) among all valid paths. If no valid path exists, return -1.

Example 1:

Input: edges = [[0,1,5],[1,3,10],[0,2,3],[2,3,4]], online = [true,true,true,true], k = 10

Output: 3

Explanation:

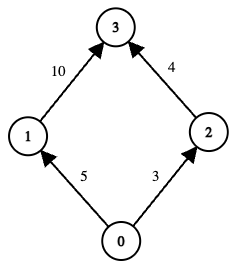
• The graph has two possible routes from node 0 to node 3:

  1. Path 0 → 1 → 3

     • Total cost = 5 + 10 = 15, which exceeds k (15 > 10), so this path is invalid.

  2. Path 0 → 2 → 3

     • Total cost = 3 + 4 = 7 <= k, so this path is valid.

     • The minimum edge\u2010cost along this path is min(3, 4) = 3.

• There are no other valid paths. Hence, the maximum among all valid path\u2010scores is 3.

Example 2:

Input: edges = [[0,1,7],[1,4,5],[0,2,6],[2,3,6],[3,4,2],[2,4,6]], online = [true,true,true,false,true], k = 12

Output: 6

Explanation:

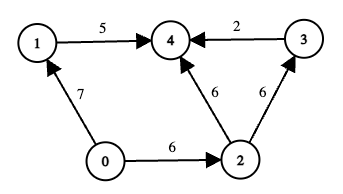
• Node 3 is offline, so any path passing through 3 is invalid.

• Consider the remaining routes from 0 to 4:

  1. Path 0 → 1 → 4

     • Total cost = 7 + 5 = 12 <= k, so this path is valid.

     • The minimum edge\u2010cost along this path is min(7, 5) = 5.

  2. Path 0 → 2 → 3 → 4

     • Node 3 is offline, so this path is invalid regardless of cost.

  3. Path 0 → 2 → 4

     • Total cost = 6 + 6 = 12 <= k, so this path is valid.

     • The minimum edge\u2010cost along this path is min(6, 6) = 6.

• Among the two valid paths, their scores are 5 and 6. Therefore, the answer is 6.

Constraints:

• n == online.length
• 2 <= n <= 5 * 104
• 0 <= m == edges.length <= min(105, n * (n - 1) / 2)
• edges[i] = [ui, vi, costi]
• 0 <= ui, vi < n
• ui != vi
• 0 <= costi <= 109
• 0 <= k <= 5 * 1013
• online[i] is either true or false, and both online[0] and online[n \u2212 1] are true.
• The given graph is a directed acyclic graph.

Constructor Summary

Constructors

Constructor	Description
Solution()

Method Summary

Modifier and Type	Method	Description
int	findMaxPathScore(int[][] edges, boolean[] online, long k)

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Details

Solution

public Solution()

Method Details

findMaxPathScore

public int findMaxPathScore(int[][] edges,
 boolean[] online,
 long k)