Class Solution
- java.lang.Object
-
- g1701_1800.s1786_number_of_restricted_paths_from_first_to_last_node.Solution
-
public class Solution extends Object
1786 - Number of Restricted Paths From First to Last Node.Medium
There is an undirected weighted connected graph. You are given a positive integer
nwhich denotes that the graph hasnnodes labeled from1ton, and an arrayedgeswhere eachedges[i] = [ui, vi, weighti]denotes that there is an edge between nodesuiandviwith weight equal toweighti.A path from node
startto nodeendis a sequence of nodes[z0, z1, z2, …, zk]such thatz0 = startandzk = endand there is an edge betweenziandzi+1where0 <= i <= k-1.The distance of a path is the sum of the weights on the edges of the path. Let
distanceToLastNode(x)denote the shortest distance of a path between nodenand nodex. A restricted path is a path that also satisfies thatdistanceToLastNode(zi) > distanceToLastNode(zi+1)where0 <= i <= k-1.Return the number of restricted paths from node
1to noden. Since that number may be too large, return it modulo109 + 7.Example 1:
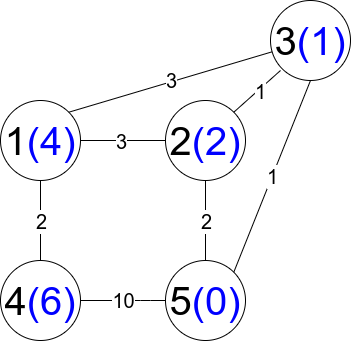
Input: n = 5, edges = [[1,2,3],[1,3,3],[2,3,1],[1,4,2],[5,2,2],[3,5,1],[5,4,10]]
Output: 3
Explanation: Each circle contains the node number in black and its
distanceToLastNode value in blue.The three restricted paths are:-
1 –> 2 –> 5
-
1 –> 2 –> 3 –> 5
-
1 –> 3 –> 5
Example 2:
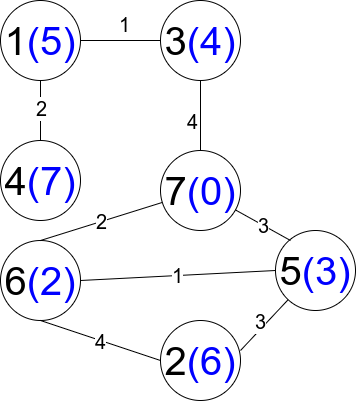
Input: n = 7, edges = [[1,3,1],[4,1,2],[7,3,4],[2,5,3],[5,6,1],[6,7,2],[7,5,3],[2,6,4]]
Output: 1
Explanation: Each circle contains the node number in black and its
distanceToLastNode value in blue.The only restricted path is 1 –> 3 –> 7.Constraints:
1 <= n <= 2 * 104n - 1 <= edges.length <= 4 * 104edges[i].length == 31 <= ui, vi <= nui != vi1 <= weighti <= 105- There is at most one edge between any two nodes.
- There is at least one path between any two nodes.
-
-
-
Constructor Summary
Constructors Constructor Description Solution()
-
Method Summary
All Methods Instance Methods Concrete Methods Modifier and Type Method Description intcountRestrictedPaths(int n, int[][] edges)
-