Package g2201_2300.s2242_maximum_score_of_a_node_sequence

Class Solution

  • public class Solution
extends Object
    2242 - Maximum Score of a Node Sequence.

    Hard

    There is an undirected graph with n nodes, numbered from 0 to n - 1.

    You are given a 0-indexed integer array scores of length n where scores[i] denotes the score of node i. You are also given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting nodes ai and bi.

    A node sequence is valid if it meets the following conditions:

    • There is an edge connecting every pair of adjacent nodes in the sequence.
    • No node appears more than once in the sequence.

    The score of a node sequence is defined as the sum of the scores of the nodes in the sequence.

    Return the maximum score of a valid node sequence with a length of 4. If no such sequence exists, return -1.

    Example 1:

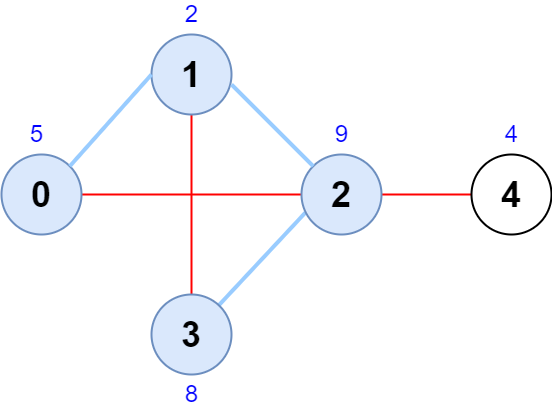
    Input: scores = [5,2,9,8,4], edges = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]

    Output: 24

    Explanation: The figure above shows the graph and the chosen node sequence [0,1,2,3].

    The score of the node sequence is 5 + 2 + 9 + 8 = 24.

    It can be shown that no other node sequence has a score of more than 24.

    Note that the sequences [3,1,2,0] and [1,0,2,3] are also valid and have a score of 24.

    The sequence [0,3,2,4] is not valid since no edge connects nodes 0 and 3.

    Example 2:

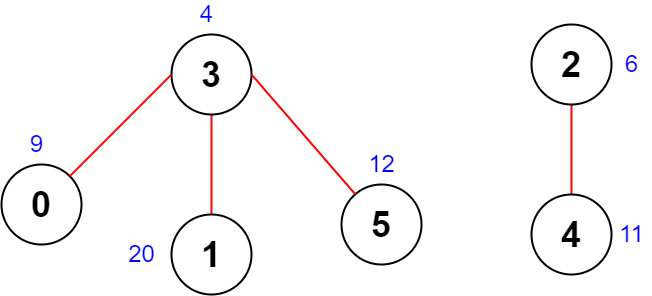
    Input: scores = [9,20,6,4,11,12], edges = [[0,3],[5,3],[2,4],[1,3]]

    Output: -1

    Explanation: The figure above shows the graph.

    There are no valid node sequences of length 4, so we return -1.

    Constraints:

    • n == scores.length
    • 4 <= n <= 5 * 104
    • 1 <= scores[i] <= 108
    • 0 <= edges.length <= 5 * 104
    • edges[i].length == 2
    • 0 <= ai, bi <= n - 1
    • ai != bi
    • There are no duplicate edges.

    • Constructor Detail

      • Solution

        public Solution()

    • Method Detail

      • maximumScore

        public int maximumScore​(int[] scores,
                        int[][] edges)