g1501_1600.s1584_min_cost_to_connect_all_points

Class Solution

java.lang.Object

g1501_1600.s1584_min_cost_to_connect_all_points.Solution

public class Solution
extends Object

1584 - Min Cost to Connect All Points.

Medium

You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].

The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val.

Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.

Example 1:

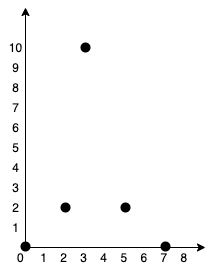
Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]

Output: 20

Explanation:

We can connect the points as shown above to get the minimum cost of 20.

Notice that there is a unique path between every pair of points.

Example 2:

Input: points = [[3,12],[-2,5],[-4,1]]

Output: 18

Constraints:

• 1 <= points.length <= 1000
• -106 <= xi, yi <= 106
• All pairs (xi, yi) are distinct.

Constructor Summary

Constructors

Constructor and Description
Solution()

Method Summary

Modifier and Type	Method and Description
void	constructMST(int[] parent, int[][] points, boolean[] mst, PriorityQueue<g1501_1600.s1584_min_cost_to_connect_all_points.Solution.Pair> pq, int[] dist)
boolean	containsFalse(boolean[] mst)
int	getDistance(int[] p1, int[] p2)
int	minCostConnectPoints(int[][] points)

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Detail

Solution

public Solution()

Method Detail

minCostConnectPoints

public int minCostConnectPoints(int[][] points)

constructMST

public void constructMST(int[] parent,
                         int[][] points,
                         boolean[] mst,
                         PriorityQueue<g1501_1600.s1584_min_cost_to_connect_all_points.Solution.Pair> pq,
                         int[] dist)

containsFalse

public boolean containsFalse(boolean[] mst)

getDistance

public int getDistance(int[] p1,
                       int[] p2)